语音参数提取特征
分帧 ——> 预增强 ——> 加窗 ——> 添加噪声 ——> FFT ——> Mel滤波 ——> 对数运算——> DCT
分帧
我们需要将不定长的音频切分成固定长度的小段,这一步称为分帧。一般取10-30ms为一帧,为了避免窗边界对信号的遗漏,因此对帧做偏移时候,要有帧迭(帧与帧之间需要重叠一部分)。 一般取帧长的一半作为帧移,也就是每次位移一帧的二分之一后再取下一帧,这样可以避免帧与帧之间的特性变化太大。通常的选择是25ms每帧,帧迭为10ms。接下来的操作是对单帧进行的。
要分帧是因为语音信号是快速变化的,而傅里叶变换适用于分析平稳的信号。在语音识别中,一般把帧长取为10~30ms,这样一帧内既有足够多的周期,又不会变化太剧烈。每帧信号通常要与一个平滑的窗函数相乘,让帧两端平滑地衰减到零,这样可以降低傅里叶变换后旁瓣的强度,取得更高质量的频谱。帧和帧之间的时间差常常取为10ms,这样帧与帧之间会有重叠,否则,由于帧与帧连接处的信号会因为加窗而被弱化,这部分的信息就丢失了。傅里叶变换是逐帧进行的,为的是取得每一帧的频谱。一般只保留幅度谱,丢弃相位谱。
预增强
预增强以帧为单位进行,目的在于加强高频。数学公式如下:
$$
s ( n ) = s ( n ) - k * s ( n - 1 ) , \quad \forall n \in \mathbb { N }
$$
k是预增强系数,范围为[0, 1),常用0.97,N是每一帧的长度,从公式可以看出每一帧的第一个数需要特殊处理。
加窗
语音在长范围内是不停变动的,没有固定的特性无法做处理,所以将每一帧代入窗函数,窗外的值设定为0,其目的是消除各个帧两端可能会造成的信号不连续性。常用的窗函数有方窗、汉明窗等,根据窗函数的频域特性,常采用汉明窗,其对应的窗函数如下:
$$
s _ { n } ^ { \prime } = ( 0.54 - 0.46 \cos ( \frac { 2 \pi ( n - 1 ) } { N - 137 } ) ) s _ { n }
$$
加窗过程其实就是将data[0:n-1]与w[0:n-1]对应相乘。
注意:预增强和加窗同时使用时,要首先进行预增强
添加随机噪声
有时候我们需要进行数据增强,会手动合成一些音频。某些人工合成(使用软件)的音频可能会造成一些数字错误,诸如underflow或者overflow。 这种情况下,通过添加随机噪声可以解决这一类问题。公式如下:
$$
s ( n ) = s ( n ) + q * r a n d()
$$
q用于控制添加噪声的强度,rand() 产生[ -1.0, 1.0 )的随机数。
注意:Kaldi中是在分帧之后的下一步添加随机噪声
fbank
人耳对声音频谱的响应是非线性的,经验表明:如果我们能够设计一种前端处理算法,以类似于人耳的方式对音频进行处理,可以提高语音识别的性能。FilterBank就是这样的一种算法。FBank特征提取要在预处理之后进行,这时语音已经分帧,我们需要逐帧提取FBank特征。
快速傅里叶变换(fft)
我们分帧之后得到的仍然是时域信号,为了提取fbank特征,首先需要将时域信号转换为频域信号。傅里叶变换可以将信号从时域转到频域。傅里叶变换可以分为连续傅里叶变换和离散傅里叶变换,因为我们用的是数字音频(而非模拟音频),所以我们用到的是离散傅里叶变换。数学公式如下:
$$
X ( k ) = \sum _ { j = 1 } ^ { N } x ( j ) w _ { N } ^ { ( j - 1 ) ( k - 1 ) }
$$
公式比较难以理解,可以想象一下傅里叶级数,一个函数可以用其他基本函数组合逼近。从公式可以看出,傅里叶变化的计算复杂度较高,因此我们通常使用的是快速傅里叶变换(fft)。
信号频率 : 组合产生复杂信号的简单信号的频率,通常简单信号平率范围很广
采样频率 : 模拟到数字的转换过程中,需要对模拟信号进行采样,每秒内的采样点数量就是采样频率
Nyquist定理(奈奎斯特): 如果想要从数字信号无损转到模拟信号,我们需要以最高信号频率的2倍的采样频率进行采样。通常人的声音的频率大概在3kHz~4kHz ,因此语音识别通常使用8k或者16k的wav提取特征。16kHz采样率的音频,傅里叶变换之后的频率范围为0-8KHz。
计算能量谱
傅里叶变换完成后,我们得到的是频域信号,每个频带范围的能量大小不一,不同音素的能量谱不一样。有两种计算方法:
- magnitude = sqrt(real*real + image*image)
- power = real*real + image*image
注意:htk同时支持这两种方式,kaldi只支持第二种
Mel滤波
Mel滤波的过程如下图:
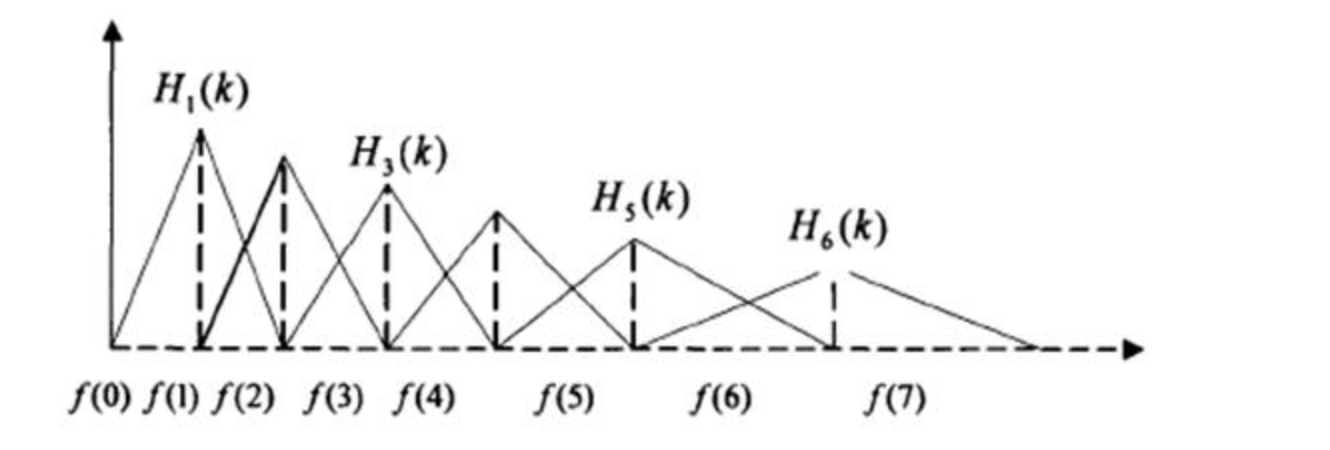
图中三角窗口表示滤波窗口。三角窗口可以覆盖从0到Nyquist的整个频率范围,通常我们会设定频率上限和下限,屏蔽掉某些不需要或者有噪声的频率范围。三角形的数量表示Mel滤波之后特征向量的维度,一般取40个。
$$
M ( b ) = \sum _ { j = 1 } ^ { b _ { j } } m e l _ { b } ( j ) * m _ { b } ( j )
$$
关于这一部分的详细情况,每个三角形对应的滤波系数可以查看
Mel系数计算, 滤波计算参考滤波计算
mel倒谱公式:
$$
M e l ( f ) = 2595 * \log _ { 10 } \left( 1 + \frac { f } { 700 } \right)
$$
对数运算
$$
M _ { \log } ( b ) = \log ( M ( b ) )
$$
这一步就是取上一步结果的对数。简单点理解,它是对纵轴的放缩,可以放大低能量处的能量差异;更深层次地,这是在模仿倒谱(cepstrum)的计算步骤。
mfcc
FBank特征已经很贴近人耳的响应特性,但是仍有一些不足:FBank特征相邻的特征高度相关(相邻滤波器组有重叠),因此当我们用HMM对音素建模的时候,几乎总需要首先进行倒谱转换,通过这样得到MFCC特征。
MFCC特征的提取是在FBank特征的基础上再进行离散余弦变换, 因此前面几步和FBank一样.
离散余弦变换(DCT)
假设做完取Log之后,我们得到N维的特征向量Mlog。离散余弦变换公式如下:
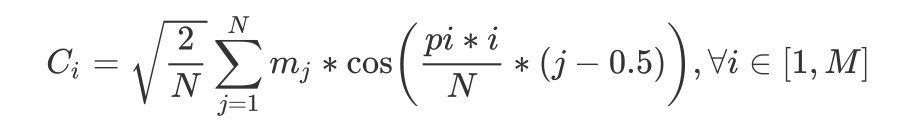
N是取Log之后的特征维度,M 是 DCT(离散余弦变换)之后的特征维度。DCT的实质是去除各维信号之间的相关性,将信号映射到低维空间。
离散余弦变换(discrete cosine transform,DCT)是傅里叶变换的一个变种,好处是结果是实数,没有虚部。DCT还有一个特点是,对于一般的语音信号,这一步的结果的前几个系数特别大,后面的系数比较小,可以忽略。上面说了一般取40个三角形,所以DCT的结果也是40个点;实际中,一般仅保留前12~20个,这就进一步压缩了数据。
均值方差归一化(CMVN)
实际情况下,受不同麦克风及音频通道的影响,会导致相同音素的特征差别比较大,通过CMVN可以得到均值为0,方差为1的标准特征。均值方差可以以一段语音为单位计算,但更好的是在一个较大的数据集上进行计算,这样识别效果会更加稳健。Kaldi中计算均值和方差的代码compute-cmvn-stats.cc, 归一化apply-cmvn.cc。
FBank与MFCC对比
- 计算量:MFCC是在FBank的基础上进行的,所以MFCC的计算量更大
- 特征区分度:FBank特征相关性较高,MFCC具有更好的判别度,这也是在大多数语音识别论文中用的是MFCC,而不是FBank的原因
使用对角协方差矩阵的GMM由于忽略了不同特征维度的相关性,MFCC更适合用来做特征。
DNN/CNN可以更好的利用这些相关性,把MFCC的离散余弦变换(DCT)省略,使用fbank特征可以更多地降低WER。
