梯度下降是最著名的优化算法之一,也是我们在训练神经网络过程中不可缺少的优化算法,了解梯度下降以及它的各种优化算法是必需的。
梯度下降形式
梯度下降有三种不同的变形形式。根据数据量的不同,在参数更新精度和训练所需时间上各有一些差异。
批梯度下降法
批梯度下降法(batch gradient descent)在整个训练集上计算损失函数关于参数$ \theta $的梯度:
$$
\theta = \theta - \eta \cdot \nabla _ { \theta } J ( \theta )
$$
因为在执行每次更新时,我们需要在整个数据集上计算所有的梯度,所以批梯度下降法的速度会很慢,并且批梯度下降法无法处理超出内存容量限制的数据集。
随机梯度下降法
与批梯度下降法相反,随机梯度下降法(stochastic gradient descent, SGD)根据每一条训练样本$ x ^ { ( i ) } $和标签$ y ^ { ( i ) } $更新参数:
$$
\theta = \theta - \eta \cdot \nabla _ { \theta } J \left( \theta ; x ^ { ( i ) } ; y ^ { ( i ) } \right)
$$
对于每一条样本SGD都更新参数,会导致目标函数出现剧烈波动。这种剧烈波动一方面会使SGD跳到潜在的更好局部最优解,但是另一方面这也使收敛过程变得缓慢复杂。
小批量梯度下降法
小批量梯度下降法最终结合了上述两种方法的优点,在每次更新时使用n个小批量训练样本:
$$
\theta = \theta - \eta \cdot \nabla _ { \theta } J \left( \theta ; x ^ { ( i : i + n ) } ; y ^ { ( i : i + n ) } \right)
$$
这种方法减少参数更新的频率可以得到更稳定的收敛效果,也可以利用最新的矩阵优化算法高效的求解小批量数据梯度。我们也将小批量梯度下降法称为SGD,下文中为了简单我们省略参数$ x ^ { ( i : i + n ) } ; y ^ { ( i : i + n ) } $。
挑战
单纯的只使用SGD会有一些问题:
- 选择一个合适的学习率可能是困难的。
- 学习率调整策略无法适应所有数据集。
- 对所有的参数更新使用同样的学习率。如果特征数据是稀疏的并且出现的频率差异很大,我们也许不想以同样的学习率更新所有的参数,对于出现次数较少的特征,我们希望使用更大的学习率。
梯度下降优化算法
动量法(momentum)
momentum是一种帮助SGD在相关方向上加速并抑制摇摆的一种方法。momentum将历史更新向量的一个分量增加到当前的更新向量中:
$$
v _ { t } = \gamma v _ { t - 1 } + \eta \nabla _ { \theta } J ( \theta )
$$
$$
\theta = \theta - v _ { t }
$$
动量项$ \gamma $通常设置为0.9。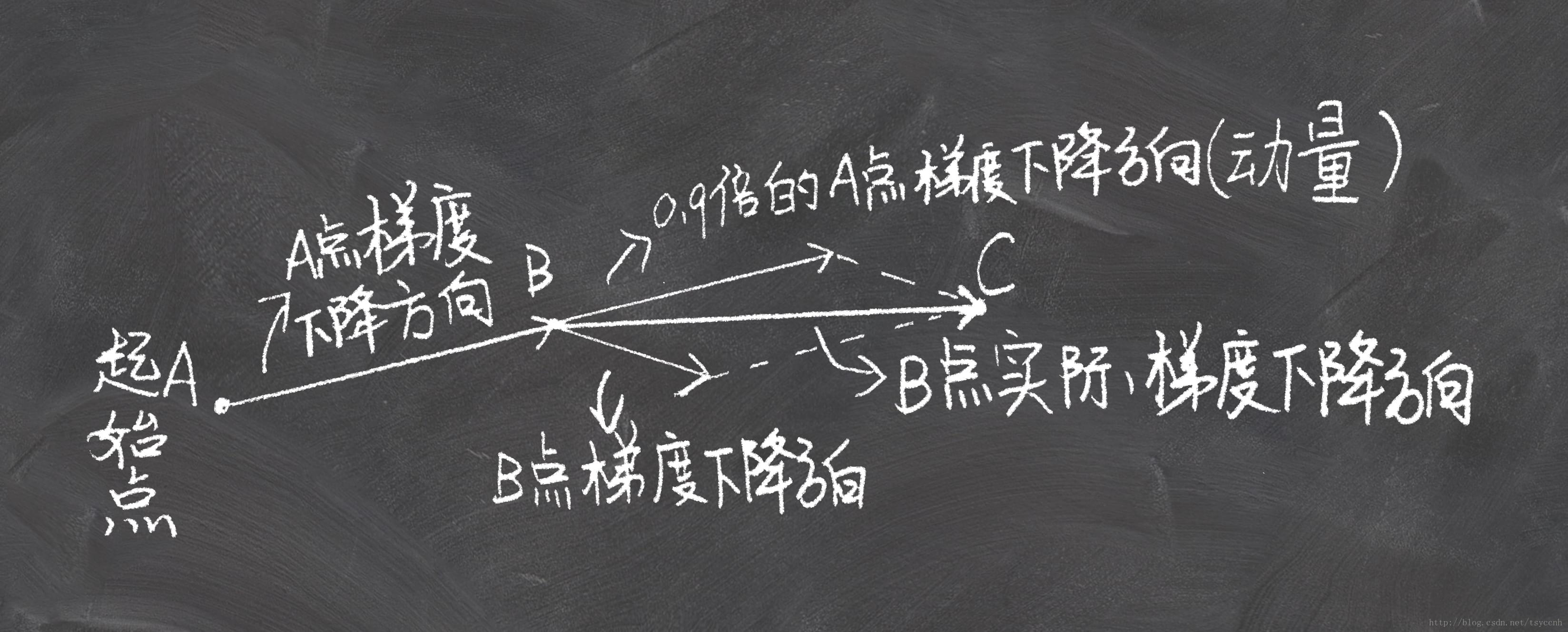
momentum就像我们从山上推下一个球,球在滚下来的过程中累积动量,变得越来越快。同样的事情也发生在参数的更新过程中:对于在梯度点处具有相同方向的维度,其动量项增大;对于在梯度点处改变方向的维度,其动量项减小。所以我们可以得到更快的收敛速度并且减少摇摆。
Nesterov加速梯度下降法
Nesterov加速梯度下降法(Nesterov accelerated gradient,NAG)是momentum的改进,是一种能够给动量项预知能力的方法:
$$
v _ { t } = \gamma v _ { t - 1 } + \eta \nabla _ { \theta } J \left( \theta - \gamma v _ { t - 1 } \right)
$$
$$
\theta = \theta - v _ { t }
$$
动量项$ \gamma $通常设置为0.9。
NAG相对于momentum,是先走到将来可能到达的点C然后在C点计算梯度,momentum是在B点计算梯度。NAG这个具有预见性的更新防止我们前进得太快,小球知道它将要去哪在遇到斜率上升时能够知道减速。
Adagrad
Adagrad可以让学习率适应参数,对于出现次数较少的特征,我们对其采用更大的学习率,对于出现次数较多的特征,我们对其采用较小的学习率。因此Adagrad非常适合处理稀疏数据如word2vec等。
Adagrad在每个时刻t对每一个参数$ \theta _ {i} $都使用不同的学习率$ \eta $。另$ g _ { t , i } $为在时刻t目标函数关于参数$ \theta _ {i} $的梯度:
$$
g _ { t , i } = \nabla _ { \theta } J \left( \theta _ { i } \right)
$$
在时刻t对每个参数$ \theta _ {i} $的更新过程为:
$$
\theta _ { t + 1 , i } = \theta _ { t , i } - \eta \cdot g _ { t , i }
$$
在时刻t基于对$ \theta _ {i} $计算过的历史梯度,Adagrad修正了对每一个参数$ \theta _ {i} $的学习率:
$$
\theta _ { t + 1 , i } = \theta _ { t , i } - \frac { \eta } { \sqrt { G _ { t , i i } + \epsilon } } \cdot g _ { t , i }
$$
其中$ G _ { t } \in \mathbb { R } ^ { d x d } $是一个对角矩阵,对角线上的元素(i,i)是到t时刻为止所有关于$ \theta _ {i} $的梯度和。$ \epsilon $是平滑项用于防止除数为0。
由于$ G _ {t} $的对角线上包含了所有关于参数$ \theta $的历史梯度平方和,所以我们可以通过$ G _ {t} $和$ g _ {t} $之间的元素向量乘法⊙向量化上述的操作:
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { \sqrt { G _ { t } + \epsilon } } \odot g _ { t }
$$
Adagrad算法的主要优点是无需手动调整学习率。它的主要缺点是在分母中累加梯度的平方,在整个训练过程中,累加的和会持续增长,这会导致学习率变小以至于最终变得无限小。
通常$ \eta = 0.01$。
RMSprop
RMSprop是Adagrad的一种扩展算法,以处理Adagrad学习速率单调递减的问题。不计算所有的梯度平方,Adadelta将计算历史梯度的窗口限制为一个固定值w。
在RMSprop中将梯度的平方递归地表示成所有历史梯度平方的均值。在t时刻的均值$ E[ g ^ { 2 }] _ { t } $只取决于先前的均值和当前的梯度(分量$ \gamma $类似于动量项):
$$
E \left[ g ^ { 2 } \right] _ { t } = \gamma E \left[ g ^ { 2 } \right] _ { t - 1 } + ( 1 - \gamma ) g _ { t } ^ { 2 }
$$
Adagrad的参数更新向量为:
$$
\Delta \theta _ { t } = - \frac { \eta } { \sqrt { G _ { t } + \epsilon } } \odot g _ { t }
$$
现在我们简单将对角矩阵$ G _ {t} $替换成历史梯度的均值$ E[ g ^ { 2 }] _ { t } $:
$$
\Delta \theta _ { t } = - \frac { \eta } { \sqrt { E \left[ g ^ { 2 } \right] _ { t } + \epsilon } } g _ { t }
$$
最终得到RMSprop的更新规则为:
$$
\theta _ {t+1} = \theta _ i - \frac{\eta}{\sqrt{E[g^2] _ t + \epsilon}} \bigodot g _ {t}
$$
通常$ \eta = 0.001$。
Adadelta
Adadelta也是一种对Adagrad的改进算法,但是其比RMSprop多了一些操作。Adadelta的作者认为RMSprop更新公式中的每个部分并不一致,即更新规则中必须与参数具有相同的假设单位。为了实现这个要求,作者首次定义了另一个指数衰减均值,这次不是梯度平方而是参数的平方的更新:
$$
E \left[ \Delta \theta ^ { 2 } \right] _ { t } = \gamma E \left[ \Delta \theta ^ { 2 } \right] _ { t - 1 } + ( 1 - \gamma ) \Delta \theta _ { t } ^ { 2 }
$$
利用$ E [ \Delta \theta ^ { 2 } ] _ { t -1 } $替换先前的更新规则中的学习率$ \eta $,最终得到Adadelta的更新规则:
$$
\theta _ {t+1} = \theta _ i - \frac{\sqrt{E[\Delta\theta^2] _ {t-1} + \epsilon}}{\sqrt{E[g^2] _ t + \epsilon}} \bigodot g _ {t}
$$
Adadelta中我们甚至不用设置初始学习率。通常$ \gamma = 0.9 $。
Adam
自适应矩估计(Adaptive Moment Estimation,Adam)是另一种自适应学习率的算法,Adam对每一个参数都计算自适应的学习率。除了像Adadelta和RMSprop一样存储一个历史平方梯度的指数衰减均值$ v _ {t} $,Adam同时还保存一个历史梯度的指数衰减均值$ m _ {t} $,类似于动量:
$$
\begin{aligned} m _ { t } & = \beta _ { 1 } m _ { t - 1 } + \left( 1 - \beta _ { 1 } \right) g _ { t } \end{aligned}
$$
$$
\begin{aligned} v _ { t } & = \beta _ { 2 } v _ { t - 1 } + \left( 1 - \beta _ { 2 } \right) g _ { t } ^ { 2 } \end{aligned}
$$
$ m _ {t} $和$ v _ {t} $分别是对梯度的一阶矩(均值)和二阶矩(方差)的估计。当 m _ {t} $和$ v _ {t} $的初始值为0向量时,Adam的作者发现它们在训练初期都偏向于0(β1和β2趋向于1),从而训练缓慢。
通过计算偏差校正的一阶矩和二阶矩估计来抵消偏差:
$$
\begin{aligned} \hat { m } _ { t } & = \frac { m _ { t } } { 1 - \beta _ { 1 } ^ { t } } \end{aligned}
$$
$$
\begin{aligned} \hat { v } _ { t } & = \frac { v _ { t } } { 1 - \beta _ { 2 } ^ { t } } \end{aligned}
$$
最终Adam的更新规则:
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { \sqrt { \hat { v } _ { t } } + \epsilon } \hat { m } _ { t }
$$
一般$ \eta = 0.001,\beta _ { 1 } = 0.9,\beta _ { 1 } = 0.999,\epsilon=1e−8 $。
AdaMax
AdaMax是Adam的一种变体。
$$
u _ t = {\lim _ {p \to +\infty}}(v _ t)^{1/p} = max(\beta _ 2u _ {t-1},|g _ {t}|)
$$
$$
m _ { t } = \beta _ { 1 } m _ { t - 1 } + \left( 1 - \beta _ { 1 } \right) g _ { t }
$$
$$
\hat { m } _ { t } = \frac { m _ { t } } { 1 - \beta _ { 1 } ^ { t } }
$$
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { u _ { t } } \odot \hat { m } _ { t }
$$
一般$ \eta = 0.002,\beta _ { 1 } = 0.9,\beta _ { 2 } = 0.999,\epsilon = 1e-8 $。
Nadam
Nadam是带有NAG项的Adam,Adam公式展开如下:
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { \sqrt { \hat { v } _ { t } } + \epsilon } \left( \frac { \beta _ { 1 } m _ { t - 1 } } { 1 - \beta _ { 1 } ^ { t } } + \frac { \left( 1 - \beta _ { 1 } \right) g _ { t } } { 1 - \beta _ { 1 } ^ { t } } \right)
$$
带进Adam的偏差校正为:
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { \sqrt { \hat { v } _ { t } } + \epsilon } \left( \beta _ { 1 } \hat { m } _ { t - 1 } + \frac { \left( 1 - \beta _ { 1 } \right) g _ { t } } { 1 - \beta _ { 1 } ^ { t } } \right)
$$
结合NAG的思想我们使用$ \hat { m } _ { t } $代替$ \hat { m } _ { t - 1 } $就得到Nadam的公式:
$$
\theta _ { t + 1 } = \theta _ { t } - \frac { \eta } { \sqrt { \hat { v } _ { t } } + \epsilon } \left( \beta _ { 1 } \hat { m } _ { t } + \frac { \left( 1 - \beta _ { 1 } \right) g _ { t } } { 1 - \beta _ { 1 } ^ { t } } \right)
$$
SGD优化算法的选择
- 各自适应学习率的优化算法表现不分伯仲,没有哪个算法能在所有任务上脱颖而出。
- 目前,最流行并且使用很高的优化算法包括SGD、带动量的SGD和Adam。
- 具体使用哪个算法取决于使用者对算法的熟悉程度,以便调节超参数。
算法可视化
SGD各优化算法在损失曲面的表现

SGD 各优化方法在鞍点的表现

参考:
An overview of gradient descent optimization algorithms
梯度下降优化算法综述
