奇异值分解SVD

发表于 | 分类于 | | 阅读次数:

在介绍奇异值分解（SVD）之前我们先来回顾一下关于矩阵的一些基础知识。

矩阵基础知识

方阵

给定一个$ n×m $的矩阵$ A $，若n和m相等也就是矩阵的行和列相等那矩阵$ A $就是一个方阵。

单位矩阵

在线性代数中，n阶单位矩阵，是一个$ n×n $的方阵，其主对角线元素为1，其余元素为0。单位矩阵以$ \mathbf { I } _ { n } $表示。

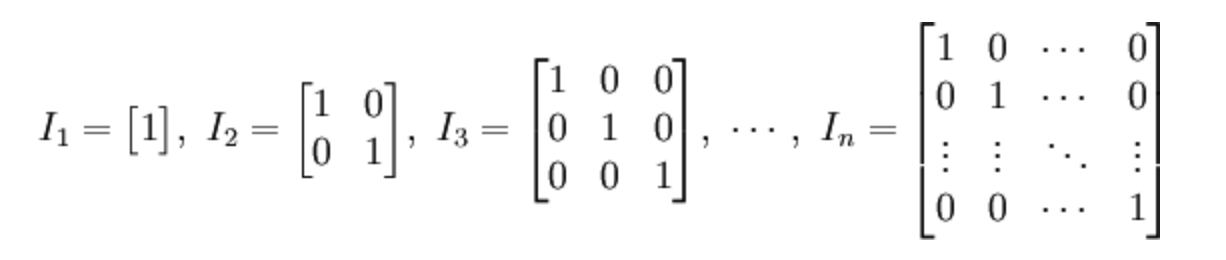
单位矩阵性质：
$$
\text { 1. } I _ { n } B _ { n \times m } = B _ { n \times m }
$$
$$
\text { 2. } B _ { n \times m } I _ { m } = B _ { n \times m }
$$
$$
\text { 3. } A _ { n } I _ { n } = I _ { n } A _ { n } = A _ { n }
$$
$$
\text { 4. } I _ { n } I _ { n } = I _ { n }
$$

转置

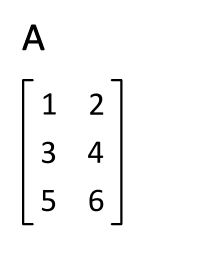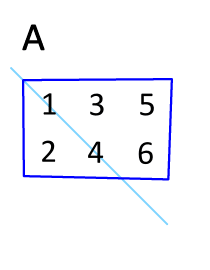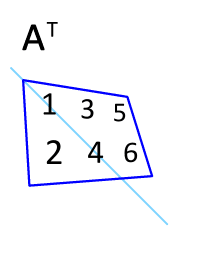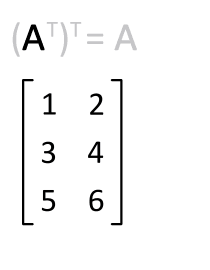
矩阵的转置是最简单的一种矩阵变换。简单来说若$ n×m $的矩阵$ A $的转置为$ A ^ { \mathrm { T } } $，则$ A ^ { \mathrm { T } } $是一个$ m×n $的矩阵并且有$ \mathbf { A } _ { i j } = \mathbf { A } _ { j i } ^ { \mathrm { T } } $。矩阵的转置相当于将矩阵按照主对角线翻转；同时，我们不难得出$ \mathbf { A } = \left( \mathbf { A } ^ { \top } \right) ^ { \top } $。

矩阵的逆

逆矩阵：在线性代数中，给定一个n阶方阵$ A $，若存在n阶方阵$ B $使得$ \mathbf { A B } = \mathbf { B } \mathbf { A } = \mathbf { I } _ { n } $，其中$ \mathbf { I } _ { n } $是n阶单位矩阵，则称$ A $是可逆的且$ B $是$ A $的逆矩阵记作$ A ^ { -1 } $。

只有方阵才可能但非必然有逆矩阵，若方阵$ A $的逆矩阵存在则称$ A $为非奇异方阵或可逆方阵。

逆矩阵性质：
$$
\text { 1. } \left( A ^ { - 1 } \right) ^ { - 1 } = A
$$
$$
\text { 2. } ( \lambda A ) ^ { - 1 } = \frac { 1 } { \lambda } \times A ^ { - 1 }
$$
$$
\text { 3. } ( A B ) ^ { - 1 } = B ^ { - 1 } A ^ { - 1 }
$$
$$
\text { 4. } \left( A ^ { \mathrm { T } } \right) ^ { - 1 } = \left( A ^ { - 1 } \right) ^ { \mathrm { T } }
$$

正交矩阵

正交矩阵是一个方阵$ Q $，其元素为实数并且行和列都为正交的单位向量，使得该矩阵的转置矩阵为其逆矩阵：
$$
Q ^ { T } = Q ^ { - 1 } \Leftrightarrow Q ^ { T } Q = Q Q ^ { T } = I
$$
其中$ I $是单位矩阵。

酉矩阵

矩阵U为酉矩阵当且仅当其共轭转置$ \boldsymbol { U } ^ { \dagger } $为其逆矩阵：
$$
U ^ { - 1 } = U ^ { \dagger }
$$
若酉矩阵的元素都是实数，其即为正交矩阵。

对称矩阵

对称矩阵是一个方阵，其转置矩阵和自身相等：
$$
A = A ^ { \mathrm { T } }
$$

对角矩阵

对角矩阵是一个主对角线之外的元素皆为0的方阵。对角线上的元素可以为0或其他值。对角矩阵都是对称矩阵。

可对角化矩阵

对角化：若方阵$ A $相似于对角矩阵，即存在可逆矩阵$ P $和对角矩阵$ Σ $，有$ A = P Σ P ^ { - 1 } $，则称A可对角化。

可对角化的充分必要条件：

$ n×n $阶矩阵$ A $可对角化的充分必要条件是矩阵$ A $有n个线性无关的特征向量。

特征值分解

特征值与特征向量

对于一个给定的方阵$ A $，它的特征向量$ v $经过这个线性变换之后，得到的新向量仍然与原来的$ v $保持在同一条直线上，但其长度或方向也许会改变。即：
$$
A v = \lambda v
$$
$ \lambda $为标量，即特征向量的长度在该线性变换下缩放的比例，称$ \lambda $为其特征值。反过来，一个实数$ \lambda $是矩阵$ A $的一个特征值，当且仅当有一个非零向量$ v $满足上面的式子。

如果特征值为正，则表示$ v $在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回零点。但无论怎样，仍在同一条直线上。

特征值分解

令$ A $是一个$ n×n $的方阵并且有n个线性无关的特征向量$ q _ { i } ( i = 1 , \dots , N ) $，这样A可以被分解为：
$$
A = Q \Sigma Q ^ { - 1 }
$$
其中，$ Q $是一个$ n×n $的方阵并且是由矩阵$ A $的特征向量组成的矩阵，$ Σ $是对角矩阵，其对角线元素为对应的特征值即$ Σ _ { i i } = \lambda _ { i } $，里面的特征值是由大到小排列的。也就是说矩阵A的信息可以由其特征值和特征向量表示。

这里需要注意只有可对角化矩阵才可以作特征分解。

特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么。

奇异值分解（SVD）

特征值分解的第一个要求就是需要矩阵是方阵，这个要求是很高的。对于一个$ n×m $的普通矩阵来说是否也可以像可对角化矩阵那样进行类似的特征值分解呢。奇异值分解（SVD）就是对普通矩阵做分解的一种方法。

假设$ M $是一个$ n×m $阶矩阵，其中的元素全部属于域$ K $，也就是实数域$ R $或复数域$ C $。如此则存在一个分解使得：
$$
M = U \Sigma V ^ { T }
$$
其中$ M $是$ n×n $阶酉矩阵，$ Σ $是$ n×m $阶非负实数对角矩阵，$ V ^ { T } $是$ V $的转置，是$ m×m $阶酉矩阵。这样的分解就称作$ M $的奇异值分解。$ Σ $对角线上的元素$ Σ _ {i,i}$即为$ M $的奇异值。$ U $和$ V $分别是$ A $的左右奇异向量矩阵。

常见的做法是将奇异值由大到小排列，这样$ Σ $便能由$ M $唯一确定了。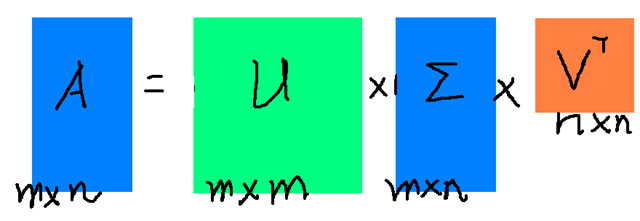

特征值分解和奇异值分解

首先，特征值只能作用在一个$ n×n $的方阵上，而奇异值分解则可以作用在一个$ n×m $的普通矩阵上。

其次，奇异值分解同时包含了旋转、缩放和投影三种作用，$ U $和$ V $都起到了对$ M $旋转的作用，而$ Σ $起到了对$ M $缩放的作用。特征值分解只有缩放的效果。

不过，这两个分解之间是有关联的。给定一个$ M $的奇异值分解，根据上面的论述，两者的关系式如下：
$$
\begin{aligned} M ^ { T } M & = V \Sigma ^ { T } U ^ { T } U \Sigma V ^ { T } = V \left( \Sigma ^ { T } \Sigma \right) V ^ { T } \end{aligned}
$$
$$
\begin{aligned} M M ^ { T } & = U \Sigma V ^ { T } V \Sigma ^ { T } U ^ { T } = U \left( \Sigma \Sigma ^ { T } \right) U ^ { T } \end{aligned}
$$
关系式的右边描述了关系式左边的特征值分解。于是：

  • $ V $的列向量（右奇异向量）是$ M ^ { T } M $的特征向量。
  • $ U $的列向量（左奇异向量）是$ M M ^ { T } $的特征向量。
  • $ \Sigma $的非零对角元（非零奇异值）是$ M ^ { T } M $或者$ M M ^ { T } $的非零特征值的平方根。

SVD的低秩逼近

奇异值$ \sigma $和特征值类似，在矩阵$ \Sigma $中奇异籽是从大到小排列的而且$ \sigma $降低的特别快，在大多数情况下前10%甚至1%的奇异值的和就占全部奇异值之和的99%以上，也就是说我们可以用前r大的奇异值来近似描述矩阵，如下：
$$
A _ { m x n } \approx U _ { n x r } \Sigma _ { r x r } V _ { r \times n } ^ { T }
$$
其中r是一个远小于m和n的数字，这样矩阵乘法看起来就是下面这个样子：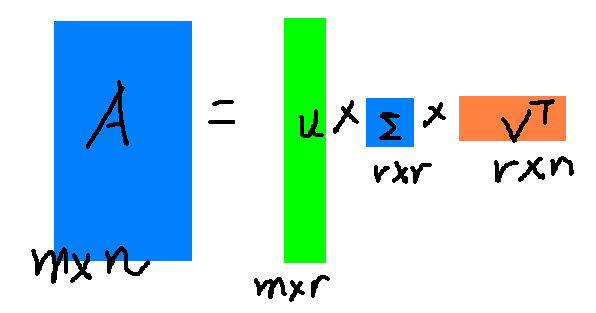

右边的三个矩阵相乘结果将会是一个接近$ A $的矩阵，r越接近n相乘的结果越接近$ A $。如果我们想要压缩空间来表示原矩阵$ A $，我们存下矩阵$ U , \Sigma , V $就好。

SVD矩阵压缩

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# -*- coding: utf-8 -*-

"""
arr =
    [[1, 2, 3, 4],
     [5, 6, 7, 8],
     [9, 10, 11, 12]]

u = 3 * 3
sigma = 3 * 4, 只返回了对角元素, 其余0元素被省略
v = 4 * 4
"""

import numpy as np

arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr)

# 1. 分解
u, sigma, v = np.linalg.svd(arr)
print(u)
print(sigma)
print(v)

# 2. 重构
new_arr = np.mat(u[:, 0:1]) * np.mat(np.diag(sigma[0:1])) * np.mat(v[0:1, :])
print(new_arr)

new_arr与arr非常接近，几乎相等。这其实是类似于图像压缩，只保留图像分解后的两个方阵和一个对角阵的对角元素，就可以恢复原图像。

SVD矩阵降维与主成分分析（PCA）

PCA就是在原始的空间中顺序地找一组相互正交的坐标轴。第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了。我们选择的r个坐标轴对空间进行压缩使得数据的损失最小。

将一个$ n \times m $的矩阵变换成一个$ n \times r $的矩阵（r < m)，这样我们就可以对列进行压缩：
$$
A _ { n \times m } P _ { m \times r } = \widetilde { A } _ { n \times r }
$$
以上就是PCA的表达公式。但是这和SVD有什么关系呢？我们知道SVD得到的奇异值也是从大到小排列的，按PCA的观点来看就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：
$$
A _ { n x m } \approx U _ { n \times r } \Sigma _ { r \times r } V _ { r \times m } ^ { T }
$$

在矩阵两边同时乘上一个矩阵$ V $得到：
$$
A _ { n \times m } V _ { m \times r } \approx U _ { n \times r } \Sigma _ { r x r } V _ { r \times m } ^ { T } V _ { m \times r }
$$
$$
A _ { n \times m } V _ { m \times r } \approx U _ { n \times r } \Sigma _ { r x r }
$$
其中$ V $就是上面PCA公式中的$ P $，这里是将一个$ n \times m $的矩阵变换到一个$ n \times r $的矩阵也就是对列进行压缩。其实我们也可以对行进行压缩：
$$
U _ { r \times n } ^ { T } A _ { n \times m } \approx \Sigma _ { r \times r } V _ { r \times m } ^ { T }
$$

可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD也就实现了PCA，而且更好的地方是，有了SVD我们就可以得到两个方向的PCA。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# coding: utf-8
import numpy as np

class PCA:
    """ 
    通过SVD分解来实现PCA
    可以选择在压缩前, 是否对数据进行中心化
    """
    def __init__(self, dimension, centered=True, compression="cols"):
        """
        dimension:      降维后的维度
        centered:       是否事先对数据进行中心化
        compression:    压缩行, 还是压缩列
        """
        self.dimension = dimension
        self.centered = centered
        self.compression = compression

    def _centered(self, train_x):
        """ 数据中心化 """
        return train_x - np.mean(train_x, axis=0)

    def _svd(self, train_x):
        """ 奇异值分解 """
        return np.linalg.svd(train_x)

    def transform(self, train_x):
        """ 数据转化(降维)
        train_x:        训练数据
        u, sigma, v:    奇异值分解结果
        result:         降维后的数据
        """
        # 1. 数据中心化
        if self.centered == True:
            train_x = self._centered(train_x)

        # 2. 奇异值分解
        u, sigma, v = self._svd(train_x)
        v = v.T
        u = u.T
        print(u.shape, sigma.shape, v.shape)

        # 3. 降维
        if self.compression == "cols":
            result = np.dot(train_x, v[:, 0:self.dimension])
        elif self.compression == "rows":
            result = np.dot(u[0:self.dimension, :], train_x)
        else:
            raise(Exception("parameter error."))
        return result

arr = np.random.rand(5, 10)
clf = PCA(2, True, "cols")
new_arr = clf.transform(arr)

0%