CTC概念
CTC算法全称叫:Connectionist temporal classification,从字面上理解它是用来解决时序类数据的分类问题的。
下图是nihao这句话的声音波形示意图,每个红色的框代表一帧数据,传统DNN训练需要知道每一帧数据对应的发音音素。比如第1,2,3,4帧对应n的发音,第5,6,7帧对应i的音素……(这里暂且将每个字母作为一个发音音素,下同)
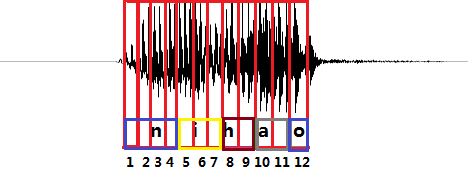
采用CTC作为损失函数的声学模型,不需要预先对数据做对齐,只需要一个输入序列和一个输出序列就可以进行训练。
CTC引入了blank(该帧没有预测值),每个预测的分类对应一整段语音中的一个spike(尖峰),其他不是尖峰的位置认为是blank。对于一段语音,CTC最后的输出是尖峰的序列,其并不关心每一个音素持续了多长时间。

进过CTC预测的序列结果在时间上可能会稍微延迟于真实发音对应的时间点,其他时间点都会被标记会blank。

这种神经网络+CTC的结构除了声学模型以外,也可以用到任何输入序列到输出序列的训练上(输入序列的长度必须大于输出序列)。比如,OCR识别也可以采用RNN+CTC来做。
CTC详情
CTC是一种损失函数,它用来衡量输入的序列数据经过神经网络之后,和真实的输出相差有多少。
对于nihao这句话,假设输入是30帧的音频数据,输出的音素长度为5。若两个人都说了nihao这句话,他们的真实输出结果都是nihao这5个有序的音素,但是因为每个人的发音特点不一样,原始的音频数据在经过神经网络计算之后,第一个人得到的结果可能是:nni…aao(长度为30),第二个人说的话得到的结果可能是:nii…aoo(长度为30),都是正确结果。可以想象长度为30的音频数据,最后可以对应上nihao这个发音顺序的结果是非常多的。CTC就是在这种序列有多种可能性的情况下,计算损失值的一种方法。
详细描述
训练集合为$ S = ( x ^ { 1 } , z ^ { 1 } ) , ( x ^ { 2 } , z ^ { 2 } ) , \ldots ( x ^ { N } , z ^ { N } ) $, 表示有N个训练样本,x是输入样本,z是对应的输出。
对于其中一个样本$ ( x , z ) , x = \left( x _ { 1 } , x _ { 2 } , x _ { 3 } , \ldots , x _ { T } \right) $表示一个长度为T帧的数据,每一帧数据是一个m维向量。$ x _ {i} $可以理解为对于一段语音,每25ms作为一帧,其中第i帧经过MFCC计算后得到的结果。$ z = \left( z _ { 1 } , z _ { 2 } , z _ { 3 } , \dots z _ { U } \right) $表示这段语音对应的正确音素。
特征x在经过RNN和softmax层之后,得到音素的后验概率矩阵y。 $ y _ { k } ^ { t } ( k = 1,2,3 , \ldots n , t = 1,2,3 , \ldots , T ) $表示在t时刻,发音为音素k的概率,其中音素的种类个数一共n个,k表示第k个音素,在一帧的数据上所有的音素概率加起来为1。即:
$$
\sum _ { t = 1 } ^ { T } y _ { k } ^ { t } = 1 , y _ { k } ^ { t } \geq 0
$$
具体过程如下图所示:
后面基于CTC的训练就是基于后验概率矩阵y得到的。
映射关系
30帧数据经过RNN前向计算之后输出的是一个30*n(n是音素个数+1,blank)的矩阵,矩阵每一列取最大值之后也是得到30个输出,那怎么和[n,i,h,a,o]这5个因素比较计算loss。
定义B变换表示简单的压缩:$ B(𝑎,𝑎,𝑏,𝑏,𝑐,𝑐,𝑑)=(𝑎,𝑏,𝑐,𝑑) $
$ 那么B(n,i,i,h,…,a,o)=(n,i,h,a,o),B(n,n,i,h,…,a,o,o)=(n,i,h,a,o)… $
但是这种变换有一个缺陷就是没法表示两个相同因素在一起的情况。解决方法就是我们前面提到的CTC中引入的blank。加入blank之后具体映射方式如下图。

通过这种映射关系,30个RNN输出就可以被映射到[n,i,h,a,o]这5个音素上。
前向后向算法bp过程见:https://blog.csdn.net/xmdxcsj/article/details/51763886
CTC原始论文见:http://www.machinelearning.org/proceedings/icml2006/047_Connectionist_Tempor.pdf
其中取log为:
$$
\begin{array} { c } { \log ( a + b ) = \log \left( a \left( 1 + \frac { b } { a } \right) \right) = \log a + \log \left( 1 + \frac { b } { a } \right) } \ { = \log a + \log \left( 1 + \exp \left( \log \left( \frac { b } { a } \right) \right) \right) = \log a + \log ( 1 + \exp ( \log b - \log a ) ) } \end{array}
$$
