softmax
对于每个样本它属于类别$ i $的概率为:
$$
y _ { i } = \frac { e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } \quad \forall i \in 1 \ldots C
$$
其中$ C $是要预测的类别数,$ a _ { i } $是模型全连接层的输出,即输出为$ a _ { 1 } , a _ { 2 } , \dots , a _ { C } $。
导数
对softmax函数进行求导,第$ i $项输出对第$ j $项输入的偏导:
$$
\frac { \partial y _ { i } } { \partial a _ { j } } = \frac { \partial \frac { e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } } { \partial a _ { j } }
$$
我们知道对于函数:
$$
f ( x ) = \frac { g ( x ) } { h ( x ) }
$$
它的导数为:
$$
f ^ { \prime } ( x ) = \frac { g ^ { \prime } ( x ) h ( x ) - g ( x ) h ^ { \prime } ( x ) } { [ h ( x ) ] ^ { 2 } }
$$
在softmax的例子中:
$$
\begin{array} { c } { g ( x ) ==> e ^ { a _ { i } } } \end{array}
$$
$$
\begin{array} { c } { h ( x ) ==> \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } \end{array}
$$
其中$ \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } $对$ a _ {j} $进行求导,结果为$ e ^ { a _ { j } } $;$ e ^ { a _ { i } } $对$ a _ { j } $进行求导要分情况进行讨论:
- 如果$ i = j $,求导结果为$ e ^ { a _ { i } } $
- 如果$ i \neq j $,求导结果为0
所以当$ i = j $时:
$$
\frac { \partial y _ { i } } { \partial a _ { j } } = \frac { \partial \frac { e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } } { \partial a _ { j } } = \frac { e ^ { a _ { i } } \Sigma - e ^ { a _ { i } } e ^ { a _ { j } } } { \Sigma ^ { 2 } } = \frac { e ^ { a _ { i } } } { \Sigma } \frac { \Sigma - e ^ { a _ { j } } } { \Sigma } = y _ { i } \left( 1 - y _ { j } \right)
$$
当$ i \neq j $时:
$$
\frac { \partial y _ { i } } { \partial a _ { j } } = \frac { \partial \frac { e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } } { \partial a _ { j } } = \frac { 0 - e ^ { a _ { i } } e ^ { a _ { j } } } { \Sigma ^ { 2 } } = - \frac { e ^ { a _ { i } } } { \Sigma } \frac { e ^ { a _ { j } } } { \Sigma } = - y _ { i } y _ { j }
$$
softmax计算与数值稳定性
我们知道$ a _ { i }$是模型输出,当$ a _ { i }$的值很大是,$ e ^ { a _ { i } } $会溢出导致softmax函数无法计算。
一种有效避免该问题的方法是让$ e ^ { a _ { i } } $中的$ a _ { i }$不要过大或者过小。在softmax函数的分式上下分别乘以一个非零常数:
$$
y _ { i } = \frac { e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } } } = \frac { E e ^ { a _ { i } } } { \sum _ { k = 1 } ^ { C } E e ^ { a _ { k } } } = \frac { e ^ { a _ { i } + \log ( E ) } } { \sum _ { k = 1 } ^ { C } e ^ { a _ { k } + \log ( E ) } }
$$
我们另$ \log ( E ) $的值为:
$$
\log ( E )= - \max \left( a _ { 1 } , a _ { 2 } , \ldots , a _ { C } \right)
$$
这样可以有效避免exp函数溢出。
CE损失函数
$$
J _ { C E } = - \sum _ { i = 1 } ^ { C } t _ { i } \log \left( y _ { i } \right)
$$
$ C $表示类别数量,$ t $是样本label,$ y $是神经网络预测值。
求导
$ J _ { C E } $对输入$ a _ { j } $的导数为:
$$
\frac { \partial l _ { C E } } { \partial a _ { j } } = - \sum _ { i = 1 } ^ { C } \frac { \partial t _ { i } \log \left( y _ { i } \right) } { \partial a _ { j } } = - \sum _ { i = 1 } ^ { C } t _ { i } \frac { \partial \log \left( y _ { i } \right) } { \partial a _ { j } } = - \sum _ { i = 1 } ^ { C } t _ { i } \frac { 1 } { y _ { i } } \frac { \partial y _ { i } } { \partial a _ { j } }
$$
其中$ \frac { \partial y _ { i } } { \partial a _ { j } } $结果上面已经求出来了:
- 当$ i = j $时:$ \frac { \partial y _ { i } } { \partial a _ { j } } = y _ { i } \left( 1 - y _ { j } \right) $
- 当$ i \neq j $时:$ \frac { \partial y _ { i } } { \partial a _ { j } } = - y _ { i } y _ { j } $
所以将结果带入上式: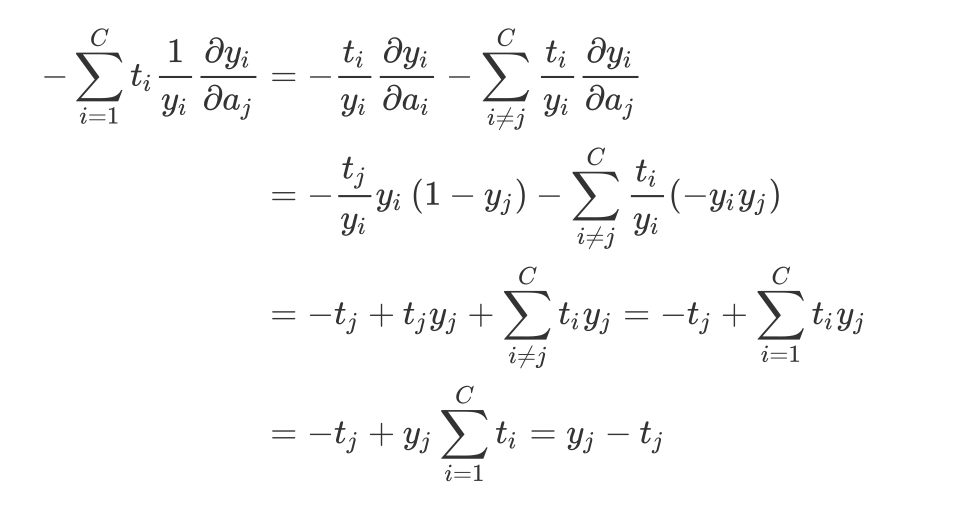
我们可以把上式改写为:
$$
\frac { \partial l _ { C E } } { \partial W } = ( y - t ) \cdot x ^ { T }
$$
$$
\frac { \partial l _ { C E } } { \partial b } = ( y - t )
$$
那么在进行随机梯度下降的时候,更新式就是:
$$
\begin{array} { l } { W \leftarrow W - \lambda ( y - t ) \cdot x ^ { T } } \end{array}
$$
$$
\begin{array} { l } { b \leftarrow b - \lambda ( y - t ) } \end{array}
$$
