viterbi算法
维特比算法说白了就是动态规划实现最短路径,只要知道动态规划是通过空间换时间的一种方法就可以了。HMM的解码部分使用的是viterbi算法。
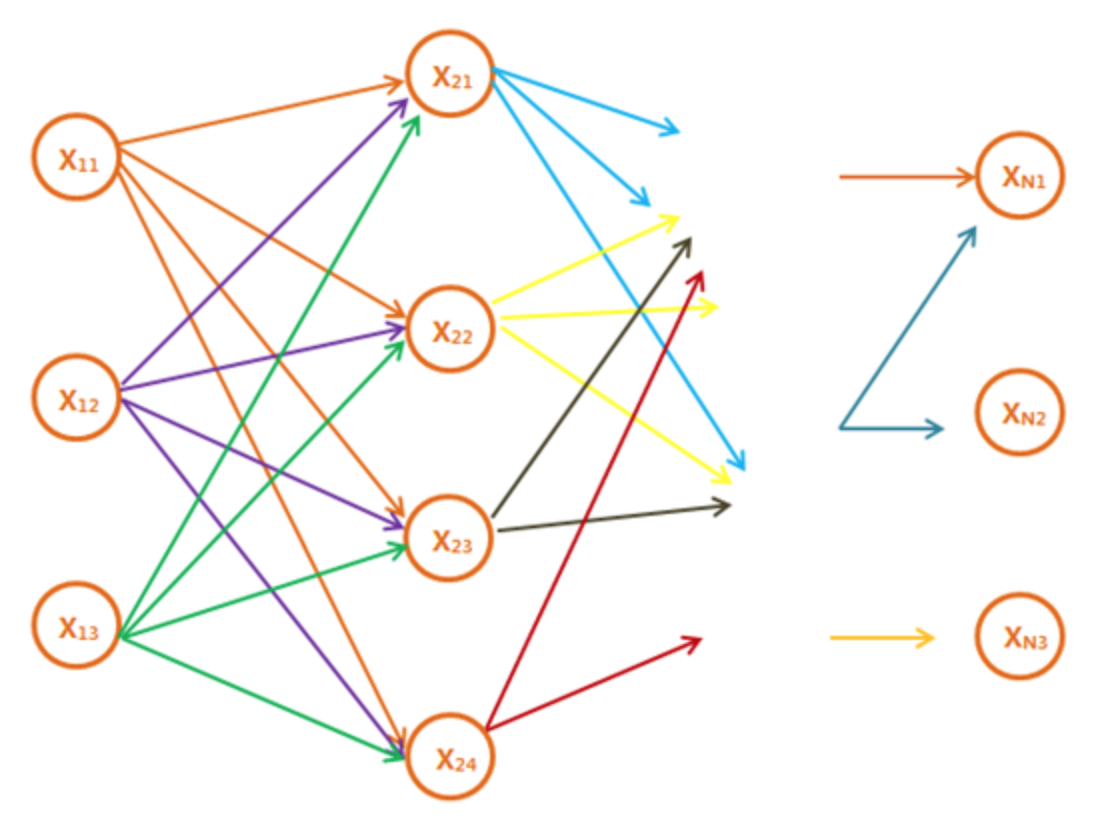
假设上图每一列分别有$ n _ {1},…,n _ {n} $个节点,如果不使用动态的话,那么计算最短路径的时间复杂度就是$ O(n _ {1} * n _ {2} * … * n _ {n}) $。
维特比算法的精髓就是,既然知道到第i列所有节点Xj{j=1,2,3…}的最短路径,那么到第i+1列节点的最短路径就等于到第i列j个节点的最短路径+第i列j个节点到第i+1列各个节点的距离的最小值。
分析一下复杂度,假设整个有向无环图中每一列节点最多有D个(也就是图的宽度为D),并且图一共有N列,那么,每次计算至多计算D*D次(i列的D个节点到i+1列D个节点的距离)。至多计算N次。那么时间复杂度为O(ND^2),远远小于穷举法O(D^N)。
前向后向算法
前向算法
前向概率
定义:给定隐尔马科夫模型$ \lambda $,定义到时刻t为止的观测序列为$ o _ {1},o _ {2},…,o _ {t} $且状态为$ q _ {i} $的概率为前向概率,记作:
$$
\alpha _ { t } ( i ) = P \left( o _ { 1 } , o _ { 2 } , \cdots , o _ { t } , i _ { t } = q _ { i } | \lambda \right)
$$
可以递推地求得前向概率$ \alpha _ {t} (i) $及观测序列概率$ p(o|\alpha ) $。
算法流程
输入:隐马尔可夫模型$ \lambda $,观测序列$ O $。
输出:观测序列概率$ p(o|\alpha ) $。
- 初始值
$$
\alpha _ { 1 } ( i ) = \pi _ { i } b _ { i } \left( o _ { 1 } \right) , \quad i = 1,2 , \cdots , N
$$
分别为初始状态概率,发射概率。
- 递推公式
$$
\alpha _ { t + 1 } ( i ) = \left[ \sum _ { j = 1 } ^ { N } \alpha _ { t } ( j ) a _ { ji } \right] b _ { i } \left( o _ { t + 1 } \right) , \quad i = 1,2 , \cdots , N
$$
大括号里面代表上层所有节点到该层特定节点的连接,然后乘以发射概率。
- 终止
$$
P ( O | \lambda ) = \sum _ { i = 1 } ^ { N } \alpha _ { T } ( i )
$$
由于到了时间T,一共有N种状态发射了最后那个观测,所以最终的结果要将这些概率加起来。
后向算法
后向概率
定义:给定隐马尔可夫模型$ \lambda $,定义在时刻t状态为$ q _ {i} $的条件下,从t+1到T的部分观测序列为$ o _ {t+1}, o _ {t+2},…,o _ {T} $的概率为后向概率,记作:
$$
\beta _ { i } ( i ) = P \left( o _ { i + 1 } , o _ { i + 2 } , \cdots , o _ { T } | i _ { t } = q _ { i } , \lambda \right)
$$
可以用递推的方法求得后向概率,$ \beta _ {t} (i) $及观测序列概率$ p(o|\lambda ) $。
算法流程
输入:隐马尔可夫模型$ \lambda $,观测序列$ O $
输出:观测序列概率$ p(o|\lambda ) $
- 初始值
$$
\beta _ { T } ( i ) = 1 , \quad i = 1,2 , \cdots , N
$$
根据定义,从T+1到T的部分观测序列其实不存在,所以硬性规定这个值是1。
- 递推公式
$$
\beta _ { t } ( i ) = \sum _ { j = 1 } ^ { N } a _ { ij } b _ { j } \left( o _ { t+1 } \right) \beta _ { t + 1} ( j ) , \quad i = 1,2 , \cdots , N
$$
$ a _ {ij} $表示状态i转移到j的概率,$ b _ {j} $表示发射$ o _ {t+1} $,$ \beta _ {t+1} (j) $表示j后面的序列对应的后向概率。
- 终止
$$
P ( O | \lambda ) = \sum _ { i = 1 } ^ { N } \pi _ { i } b _ { i } \left( o _ { 1 } \right) \beta _ { 1 } ( i )
$$
最后的求和是因为,在第一个时间点上有N种后向概率都能输出从2到T的观测序列,所以乘上输出O1的概率后求和得到最终结果。
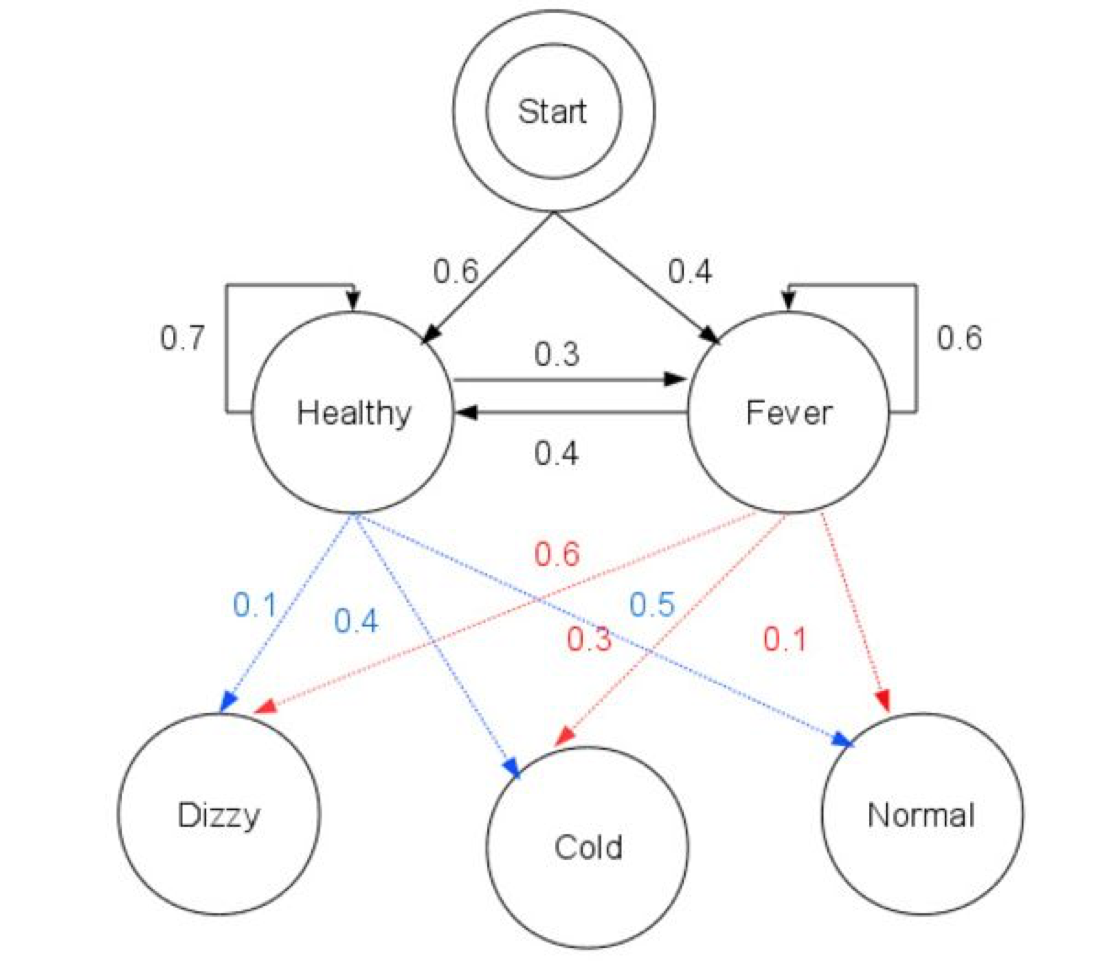
HMM模型的三个基本问题
给定一个模型,如何计算某个特定的输出序列的概率?
Forward-Backward算法给定一个模型和某个特定的输出序列,如何找到最可能产生这个输出的状态序列?
维特比算法给定足够量的观测数据,如何估计隐含马尔可夫模型的参数?
baum-welch算法
